© 2008 г. А. Н. Озерин, Т. С. Куркин, Л. А. Озерина, В. Ю. Долматов
ЗАО “Алмазный центр”, Санкт — Петербург Поступила в редакцию 21.12.2006 г.
Методами измерения рентгеновского рассеяния в больших и малых углах изучена структура и пространственное строение агрегатов наноалмазов, полученных методом детонационного синтеза. Определены эффективные размеры кристаллитов и функция распределения кристаллитов по размерам. Выполнено восстановление формы рассеивающих агрегатов по данным малоуглового рентгеновского рассеяния. На основании полученных результатов сделан вывод о том, что агрегаты наноалмазов представляют собой протяженные пространственные структуры, построенные из 9 — 10 кластеров, каждый из которых включает в себя 4 — 5 кристаллитов с кристаллической решеткой типа алмаза.
ВВЕДЕНИЕ
Наноалмазы, полученные методом детонационного синтеза (НАДС), являются перспективным материалом для ряда важных практических применений [1]. Однако его широкое применение осложняется тем, что НАДС в процессе синтеза образуют агрегаты и кластеры, пространственное строение и структура которых, несмотря на интенсивные работы в этой области [1 — 10], остаются в значительной степени невыясненными.
Целью данной работы являлось изучение особенностей пространственного строения НАДС методами дифракции рентгеновского излучения под большими и малыми углами рассеяния и восстановление формы единичных агрегатов НАДС по данным малоуглового рентгеновского рассеяния.
ОБЪЕКТЫ И МЕТОДЫ ИССЛЕДОВАНИЯ
В работе исследовали представительную серию из семи образцов НАДС, различающихся условиями синтеза, очистки и исходным агрегатным состоянием. Характеристики образцов приведены в таблице.
Рентгенографические измерения в больших углах дифракции выполняли для сухих порошков НАДС (таблица) (препараты образцов НАДС1 — НАДС3 получали высушиванием исходных водных дисперсий), малоугловые измерения проводили для водных дисперсий НАДС (препараты образцов НАДС4 — НАДС7 готовили редиспергированием исходных порошков в деионизованной воде).
Дифрактограммы в больших углах рассеяния регистрировали на дифрактометре D8 фирмы “Brncker” с фокусирующим германиевым кристаллом — монохроматором на первичном пучке (СиКа1 — излучение) методом съемки “на просвет” в диапазоне углов рассеяния 20 = 10° — 100° с вращением образца, помещенного между тонкими пленками из аморфного полиэтилентерефталата. Для нахождения функции распределения кристаллитов по размерам использовали модифицированный метод фурье — анализа профиля рентгеновской дифракционной линии [11, 12].
Кривые малоуглового рентгеновского рассеяния исследуемых систем измеряли на дифрактометре КРМ — 1 со щелевой схемой коллимации первичного пучка (СиКа — излучение, Ni — фильтр, сцинтилляционный детектор). Исследуемые суспензии НАДС помещали в стеклянные капилляры фирмы Хильгенберг диаметром 1.5 мм. В качестве координаты рассеяния использовали величину модуля вектора рассеяния х = 4пsin(0)/X, где 20 — угол рассеяния, X = 1.542 А — длина волны излучения. Интенсивность рассеяния регистрировали в диапазоне значений s 0.007 — 0.426 А-1. Предварительную обработку исходных кривых рассеяния (сглаживание, нормировка), учет паразитного рассеяния и рассеяния буфером, а также внесение коллимационных поправок проводили с помощью комплекса программ SYRENA [13] и GNOM [14].
Характеристики НАДС
| Обозначение | Год производства, производитель | Среда подрыва заряда (сплав тротила с гексогеном ~ 50/50) | Марка по ТУ | Агрегатноесостояние | Примечание |
| НАДС1 | 1998a | Газовая среда | АСДУв | Водная суспензия | Очистка CrO3 + H2SO4 |
| НАДС2 | 1998б | Водная среда | УДД-ТАНг | Водная суспензия | Очистка HNO3 (p ~ 80 атм, t ~ 240°C) |
| НАДС3 | 2006б | Водная среда | УДД-ТАНг | Водная суспензия | Очистка HNO3 (p ~ 80 атм, t ~ 240°C), последующая обработка HCl |
| НАДС4 | 2004б | Водная среда | УДД-СТПг | Порошок | Очистка HNO3 (p ~ 80 атм, t ~ 240°C) |
| НАДС5 | 2004б | Водная среда с гидразином | УДД-СТП-ГГ опытная партия | Порошок | Очистка HNO3 (p ~ 80 атм, t ~ 240°C) |
| НАДС6 | 2004б | Водная среда с аммиаком | УДД-СТП-АМ опытная партия | Порошок | Очистка HNO3 (p ~ 80 атм, t ~ 240°C) |
| НАДС7 | 2004б | Водная среда с мочевиной | УДД-СТП-МО опытная партия | Порошок | Очистка HNO3 (p ~ 80 атм, t ~ 240°C) |
a РФЯЦ — ВНИИТФ (г. Снежинск), предоставлено Чухаевой С.И. 6 ЗАО “Алмазный центр” (г. Санкт — Петербург). в ТУ 2 — 037 — 677- 94. г ТУ 05121441 — 275 — 95.
Для определения формы и пространственного строения рассеивающих частиц использовали подход, основанный на применении хорошо обоснованных алгоритмов восстановления формы рассеивающих частиц по данным малоуглового рентгеновского рассеяния, реализованный в программе DAMMIN [15], алгоритм которой использует метод Монте — Карло с наложением процедуры “отжига” для восстановления формы рассеивающей частицы в рамках модели “виртуальных” (dummy) атомов. Данный подход восстанавливает форму частицы с низким разрешением, поскольку сам метод малоуглового рассеяния является методом низкого разрешения и обеспечивает получение структурной информации только в диапазоне ~ 10 — 1000 А. Тем не менее информативность такого подхода была ранее убедительно продемонстрирована для большого ряда систем различной природы: биологических макромолекул [15], элементоорганических [16] и неорганических [17] наночастиц сверхразветвленного строения. Отметим, что данный подход восстанавливает форму рассеивающих частиц, усредненную по всему их ансамблю, присутствующему в облучаемом объеме, а не форму какой — то одной индивидуальной частицы ансамбля.
Форму рассеивающих частиц восстанавливали как без каких — либо начальных ограничений их симметрии (точечная группа P1), так и для условия наложения определенной пространственной симметрии на конечное решение (P2, P22, P3, P23, P43). Вычисления по программе DAMMIN проводили в “быстрой” (меньшее число “виртуальных” атомов), а также в “экспертной” моде, с увеличением количества “виртуальных” атомов примерно на один десятичный порядок, по сравнению с “медленной” модой. Усреднение восстановленных в индивидуальных прогонах структур проводили с помощью программ DAMAVER и SUPCOMB [18]. Для каждой кривой рассеяния выполняли как минимум десять восстановлений перед последующим усреднением. Для трехмерного графического представления полученных структур использовали программу MASHA [19]. Все перечисленные программы обработки данных малоуглового рентгеновского рассеяния являются частью программного комплекса ATSAS 2.0
Фрактальную размерность агрегатов рассеивающих частиц df или ds определяли известным способом [20] из наклона соответствующего линейного участка кривой рассеяния, представленной в координатах lg(I(s))-lg(s).
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Дифрактограммы в больших углах рассеяния для всех исследованных порошковых образцов НАДС оказались идентичными друг другу в пределах экспериментальной ошибки. В качестве примера на рис. 1 приведена типичная дифрактограмма одного из исследованных образцов, где наблюдаемые рефлексы отвечают решетке типа алмаза с параметром a = (3.565 ± 0.005) А.
Нормированные профили первого сильного рефлекса 111 для всех семи типов исследованных НАДС представлены на рис. 2. Видно, что профили рефлексов практически идеально совпадают между собой, что позволяет усреднить индивидуальные дифрактограммы и выполнять последующий профильный анализ с единственной дифрактограммой “среднего” НАДС.
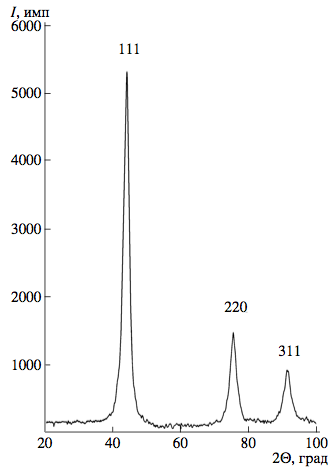
Рис. 1. Дифрактограмма в больших углах рассеяния порошкового образца НАДС.
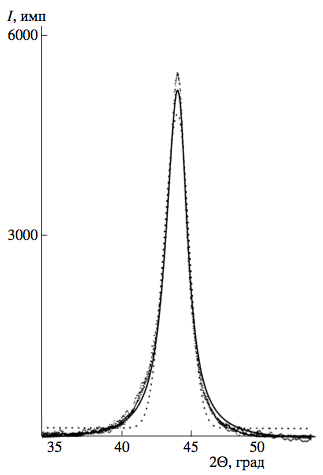
Рис. 2. Профили рефлекса 111 для всех исследованных образцов НАДС. Сплошная линия — аппроксимация профилей суммой функций Гаусса и Лорентца, пунктирная — функцией Гаусса.
Оптирование “среднего” профиля рефлекса 111 известными профильными функциями (Гаусс, Лоретнц, смешанный Гаусс — Лорентц, Пирсон VII, Фойгт) показало, что наилучшее приближение достигается при использовании суммы функций Гаусса и Лорентца, в то время как индивидуальная функция Гаусса дает неудовлетворительный результат (рис. 2).
Известно [21], что если профиль линии описывается функцией Лауэ вида I(S) = sin2(nSa)/(nSa)2, где S = 2sin(0)/X, то в распределении кристаллитов по размерам будут представлены только кристаллиты с размером l = а, т.е. функцией распределения в этом случае должна быть 8 — функция. Поскольку профильная функция Гаусса достаточно хорошо отражает особенности профильной функции Лауэ, несовпадение экспериментального профиля рефлекса на рис. 2 с функцией Гаусса указывает на существование некоторой функции распределения кристаллитов по размерам (РКР) для исследуемых НАДС.
Рассчитанные согласно [11, 12] среднечисловые Nn и средневесовые (объемные) Nv функции РКР для НАДС приведены на рис. 3. Средние по РКР значения (Nn), (Nv) и полидисперсности распределения D = (Nv)/{Nn) составили 39.48 А, 1.23 для НАДС и 39.42 А, 1.07 для профильной функции Гаусса, соответственно. Поскольку рефлекс 222 (20 = 97°) в структуре алмаза является запрещенным по правилам погасания, учесть влияние искажений и нарушений решетки на рассчитанные РКР в данном случае не представлялось возможным.
Полуширина экспериментального рефлекса 111 НАДС (рис. 2) составила А111 = 1.76° (в шкале 20) или AS111 = 3.69 х 10-2 А-1 в шкале S. Для профильной функции Гаусса (рис. 2) А = 2.26° и AS = 4.74 х 10 2 А 1 соответственно. Эффективный размер кристаллита l111, рассчитанный по соотношению Шеррера 1Ш = KX/(Ahkl cos(0№)), где константа K определяется форм — фактором кристаллита, равнялся 54 А (K = 1) и 49 А (K = 0.9) для НАДС, 42 А (K = 1) и 38 А (K = 0.9) для профильной функции Гаусса (рис. 2) соответственно.
Значение l = 42 А (K = 1) для профильной функции Гаусса совпадает со средним значением (Nv) из функции РКР, что является ожидаемым результатом [11, 12].
Для НАДС совпадение значений (Nv) и 1щ достигается только при условии K = 0.9 (48 и 49 А соответственно).
Эффективный размер кристаллитов НАДС для других кристаллографических направлений составил l220 = 47 А (K = 1) и 43 А (K = 0.9); l311 = 51 А (K = 1) и 46 А (K = 0.9).
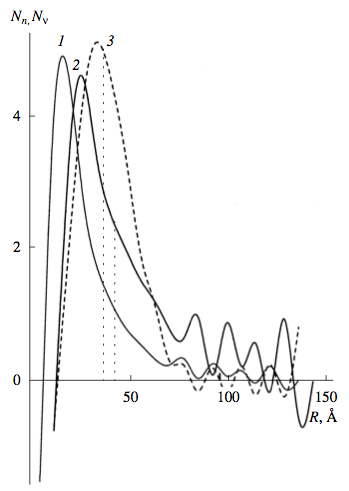
Рис. 3. Среднечисловые Nn (I) и средневесовые (объёмные) Nv (2, 3) фнкции РКР для НАДС. Кривая 3 соответствует профильной функции Гаусса на рис. 2
Эффективный размер кристаллитов НАДС для других кристаллографических направлений составил l220 = 47 А (K = 1) и 43 А (K = 0.9); l311 = 51 А (K = 1) и 46 А (K = 0.9).
При расчете приведенных выше эффективных размеров кристаллитов для НАДС поправку на инструментальное уширение профиля линии не вносили ввиду ее малости. Как и в случае расчета функций РКР, выполнить оценку влияния искажений и нарушений решетки на рассчитанные величины размеров кристаллитов не представлялось возможным.
Из найденных значений эффективных размеров кристаллитов в различных кристаллографических направлениях в предположении призматической формы кристаллитов был оценен объем единичного кристаллита НАДС (8 х 104 А3).
Информацию о сборке кристаллитов НАДС в кластеры и агрегаты большего размера и их пространственной структуре получали из данных малоуглового рентгеновского рассеяния.
Нормированные друг на друга кривые малоуглового рассеяния для всех исследованных в виде водных суспензий образцов НАДС показаны на рис. 4. Поскольку концентрация суспензий была мала (около 8 мас. % или 2.3 об. % для плотности НАДС 3.52 г/см3), влиянием межчастичной интерференции в нашем случае можно было пренебречь, что позволяло интерпретировать индивидуальные кривые малоуглового рассеяния как рассеяние от индивидуальных невзаимодействующих пространственных структур (агрегатов).
Как и для рассеяния под большими углами, кривые малоуглового рассеяния всех исследованных образцов НАДС после взаимной нормировки оказались идентичными друг другу. По этой причине для целей дальнейшего анализа использовали единую “усредненную” кривую малоуглового рассеяния НАДС (рис. 4).
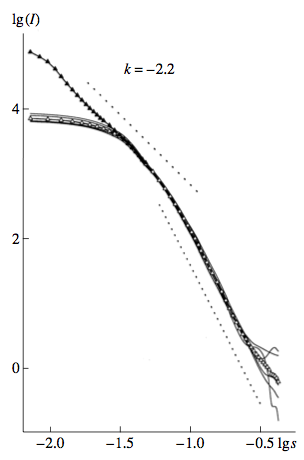
Рис. 4. Кривые малоугловые рассеявания для всех использованных образцов НАДС. Сплошные линии — индивидуальные кривые, залитые точки — усреднённая кривая рессеяния, открытые точки — рассеяния от выделенной субструктуры. Пунктирные линии соответствуют областям линеарицзации кривой рассеяния, значения параметра К характеризуют тангенс угла наклона линейных участков.
Вид кривой малоуглового рассеяния НАДС является типичным для так называемых “двухуровневых” структур с иерархией соответствующих структурных уровней [22, 23], каждый из которых характеризуется своими собственными радиусом инерции Rg и массовой фрактальностью df или поверхностной фрактальностью ds рассеивающего объекта (уровня). Для кривой из рис. 4 значения этих параметров, найденные согласно изложенному в [22, 23] подходу, составили 154 А, df = 2.2 (массовый фрактал) и 48 А, ds = 2 (компактная частица с резкими фазовыми границами и небольшим переходным слоем) для первого верхнего и второго нижнего структурных уровней, соответственно. Вклад первого структурного уровня в суммарную интегральную интенсивность малоуглового рассеяния незначителен, что следует из представленных на рис. 5 в координатах Кратки Is2 — s кривых малоуглового рассеяния, где площадь под соответствующими кривыми пропорциональна вкладу от того или другого уровня в интегральную интенсивность.
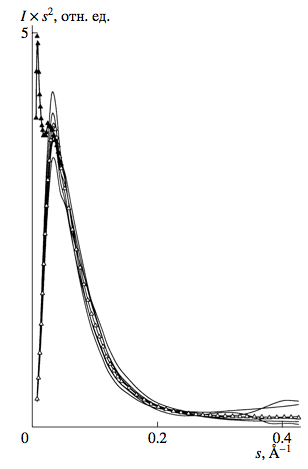
Рис. 5. Кривые малоуглового рассеяния в координатах Is2 — s для всех исследованных образцов НАДС. Сплошные линии — индивидуальные кривые, залитые точки — усредненная кривая рассеяния, открытые точки — рассеяние от выделенной субструктуры.
Анализируемые системы не являются аддитивной смесью рассеивающих частиц с разными характерными размерами, поскольку кривые рассеяния оказались идентичными друг другу для образцов с самой различной предысторией. Более того, предварительные результаты показали, что структура таких частиц сохраняется без изменения даже в случае их введения в полимерную матрицу в качестве наполнителя. Все это позволяет заключить, что для исследуемых образцов НАДС картина малоуглового рентгеновского рассеяния отвечает рассеянию на так называемых “неразрушаемых” агрегатах [1, 9], изучение структуры которых и является предметом данной работы.
Данные, представленные на рис. 4 и 5, позволяют выделить составляющую рассеяния, обусловленную рассеянием на субструктурах второго (нижнего) иерархического уровня, которая была проанализирована в первую очередь.
Известно [13], что малоугловое рассеяние разбавленной системой частиц может быть интерпретировано с минимальной детализацией (усложнением) рассеивающей системы либо в приближении рассеяния от полидисперсной системы частиц с известным форм — фактором (шары, призмы, объемные эллипсоиды вращения и т.д.), либо в приближении рассеяния от идентичных частиц неизвестной формы и пространственного строения. В первым случае конечным результатом интерпретации данных малоуглового рассеяния является восстановленная функция распределения частиц по размерам, во втором — определение формы и размера частицы.
Предположение о том, что рассеяние на субструктурах второго уровня обусловлено рассеянием на полидисперсной системе частиц простой формы, не может быть, по нашему мнению, хорошо обосновано. Действительно, отмеченная выше идентичность всех кривых малоуглового рассеяния означала бы в этом случае сохранение неизменной функции распределения частиц по размерам для НАДС самой различной предыстории, что является маловероятным. Рассчитанная, согласно процедуре GNOM [14] из кривой рассеяния субструктурой второго уровня (рис. 4), функция распределения DV частиц по размерам для простейшей модели полидисперсных рассеивающих частиц в форме шаров является узкой (рис. 6). По этой причине для дальнейшего анализа была выбрана интерпретация малоуглового рассеяния в приближении рассеяния от идентичных частиц неизвестной формы и пространственного строения.
Для рассеивающего объекта в виде разбавленной системы идентичных частиц в условиях исключения межчастичной интерференции экспериментально определяемая интенсивность рассеяния представляет собой усредненную по всем ориентациям интенсивность рассеяния одной частицей, что позволяет определить ряд ее структурных характеристик.
В этом случае удобно ввести понятие корреляционной функции частицы у(г), определяемой как усредненная самосвертка распределения плотности р(г) в частице [13] и связанную с ней так называемую функцию распределения расстояний в частице p(r) = Y(r)r2. Для однородных (без внутренних полостей) частиц функция p(r) имеет колоколообразный вид, а ее максимум отвечает некоторому “среднему” радиусу частицы [13]. Обе эти функции связаны как с геометрией частицы (они количественно описывают набор отрезков, соединяющих элементы объема частицы), так и с распределением внутричастичных неоднородностей. В случае однородной частицы значение функции p(r) равно числу отрезков длины г, соединяющих два произвольных элемента объема частицы.
Рассчитанная в соответствии с процедурой GNOM [14] для рассеяния на субструктурах второго уровня НАДС функция p(r) приведена на рис. 6. Вид функции p(r) является характерным [13] для компактных частиц с невысокой степенью анизометричности формы.
Дополнительная информация о пространственном строении рассеивающих частиц субструктуры второго уровня были получены с помощью комплекса программ [15, 18], использующих представление формы частицы с помощью модели “виртуальных” атомов. Результаты восстановления формы рассеивающих частиц субструктуры из кривых малоуглового рассеяния для НАДС приведены на рис. 7 (группа 2). Форму рассеивающих частиц восстанавливали как без каких — либо начальных ограничений их симметрии (точечная группа P1), так и для условия наложения определенной пространственной симметрии на конечное решение (P2, P22, P3, P23, P43). Среднее значение величины исключенного объема частицы субструктуры составило 4 х 105 А3.
К сожалению, выбрать какую — либо из восстановленных форм группы 2 на рис. 7 в качестве основной по количественным критериям оказалось невозможным, поскольку рассчитанная интенсивность малоуглового рассеяния от всех моделей этой группы очень хорошо согласовывалась с экспериментальной интенсивностью рассеяния (рис. 8). Для дифференциации и отбора соответствующей формы в качестве основной необходимо продлить диапазон измерения экспериментальной интенсивности рассеяния до больших значений координаты s.
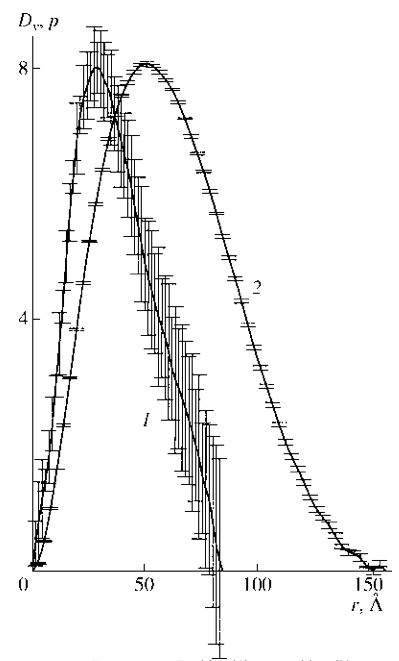
Рис. 6. Функции Dy(r) (1) и p(r) (2) для выделенной субструктуры НАДС.
Вместе с тем, модель, восстановленная при наложении условия симметрии P23 (группы 2 и 3 на рис. 7), представляется достаточно интересной для последующего анализа. Действительно, сопоставление объема частицы субструктуры, найденного из данных по малоугловому рассеянию, с объемом единичного кристаллита, оцененного из рентгенографических измерений в больших углах дифракции, показывает, что частица субструктуры может состоять из (4 х 105)/(8 х 104) А3 = 5 кристаллитов, т.е. представлять собой кластер кристаллитов. Наиболее естественной формой такого кластера является форма, восстановленная при наложении условия симметрии Р23, которая легко приводится к системе пяти эквивалентных тетраэдров (группа 3 на рис. 7). Подобная симметрия является типичной для кристаллов алмаза, хотя ее справедливость для нанодисперсного кластера несомненно требует дополнительного подтверждения.
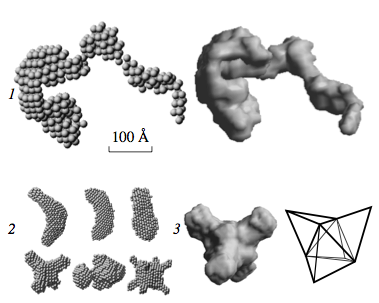
Рис. 7. Форма рассеивающих частиц НАДС: “неразрушаемый агрегат” (группа моделей 1); частицы субструктуры, восстановленные при наложении условия симметрии P1, P2, P22, P23, P3, P432 (группа 2); увеличенное изображение формы, восстановленной при наложения условия симметрии P23 (группа 3). Визуализация моделью объемных шаров (1, 2) и моделью “поверхности, доступной растворителю” (1, 3). Масштаб линейных размеров указан для групп 1 и 2.
Аналогичная процедура восстановления формы была выполнена и для всей кривой малоуглового рассеяния НАДС (рис. 4, 8), которая представляет собой рассеяние “неразрушаемым агрегатом” НАДС. Форму рассеивающей частицы в этом случае восстанавливали без каких — либо начальных ограничений их симметрии (точечная группа P1). Результаты восстановления формы “неразрушаемого агрегата” приведены на рис. 7 (группа 1). Рисунок 8 демонстрирует хорошее согласие рассчитанной интенсивности малоуглового рассеяния модельной частицей с экспериментальной интенсивностью рассеяния. Среднее значение величины исключенного объема “неразрушаемого агрегата” составило 3.5 х 106 А3, что соответствует (3.5 х 106)/(4 х 105) А3 ~ 9 — 10 кластерам, составляющим агрегат НАДС.
Здесь следует добавить, что определенная выше (рис. 4) для НАДС фрактальная размерность агрегата df = 2.2 близка к значению df = 2.1, характерному [20] для роста фрактального агрегата по механизму “химически лимитированной” или “реакционно лимитированной” кластер — кластерной агрегации, что вполне соответствует условиям синтеза НАДС детонационным способом.
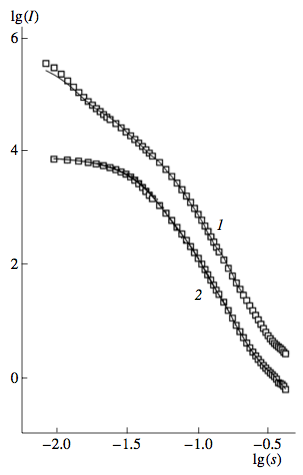
Рис. 8. Кривые малоуглового рассеяния “неразрушаемым агрегатом” (1) и субструктурой (2) НАДС. Точки — экспериментальная интенсивность, линии — интенсивность, рассчитанная от моделей соответствующей группы на рис. 7. Для удобства представления кривая 2 сдвинута вверх относительно кривой 1.
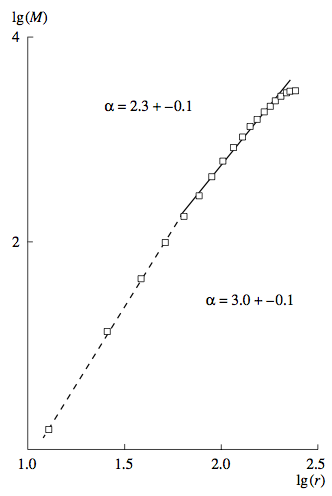
Рис. 9. Рис. 4. Зависимости lg(M)-lg(r) для восстановленной структуры “неразрушаемого агрегата” из рис. 7.
В завершении отметим, что знание пространственных координат виртуальных атомов в структурах на рис. 7 дает возможность прямым суммированием найти эффективную функцию радиального распределения плотности в частице p(r), интегрирование которой в сферической системе координат позволяет оценить фрактальные размерности частиц из известного соотношения скейлинга M = rа между массой частицы M и ее характерным размером r (рис. 9). Найденные значения параметра скейлинга а = 3 в области малых линейных размеров в агрегате НАДС (рис. 9) хорошо согласуются с выводом, сделанным выше из данных рис. 4 о плотном компактном строении частиц, составляющих второй низкий уровень иерархической пространственной структуры НАДС, в то время как при больших линейных размерах агрегат НАДС проявляет себя как типичный массовый фрактал, параметр скейлинга которого а = 2.3 в пределах экспериментальной ошибки определения совпадает с фрактальной размерностью агрегата df = 2.2 найденной из кривых малоуглового рассеяния (рис. 4). Выполненное сопоставление данных о фрактальной размерности агрегата НАДС подтверждают непротиворечивость и самосогласованность результатов восстановления формы рассеивающих частиц, полученных в данной работе.
Таким образом, результаты данной работы показывают, что агрегаты НАДС, полученные методом детонационного синтеза, представляют собой протяженные пространственные структуры, построенные из 9 — 10 кластеров, каждый из которых включает в себя 4 — 5 кристаллитов с кристаллической решеткой типа алмаза. Отдельные элементы структуры, подтверждающие предлагаемую нами модель строения агрегата НАДС, можно найти в опубликованной недавно в [9].
Обнаружено, что НАДС различной предыстории (время хранения, условия получения и очистки) проявляют удивительную “инвариантность” структуры и структурных параметров, определяемой рентгенографическими методами. Возможно, что подобная “инвариантность” определяется сходными условиями синтеза исследованных НАДС (объем камеры, состав и вес заряда и т.п.). Данный вопрос предполагается исследовать в дальнейшем более подробно.
Результаты работы имеют важное значение для поиска новых областей практического применения НАДС.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 05 — 03 — 33120).
СПИСОК ЛИТЕРАТУРЫ
- Долматов В.Ю. // Успехи химии. 2001. Т. 70. № 7. С. 687.
- Байдакова М.В., Вулъ А.Я., Сиклицкий В.И, Фалеев Н.Н. // ФТТ. 1998. Т. 40. № 4. С. 776.
- Алексенский А.Е., Байдакова М.В., Вулъ А.Я., Сиклицкий В.И. // ФТТ. 1998. Т. 41. № 4. С. 740.
- Неверовская А.Ю., Возняковский А.П., Долматов В.Ю. // ФТТ. 2004. Т. 46. № 4. С. 646.
- Кулакова И И. // ФТТ. 2004. Т. 46. № 4. С. 621.
- Чухаева С И. // ФТТ. 2004. Т. 46. № 4. С. 610.
- Долматов В.Ю, Веретенникова М.В, Марчуков ВА, Сущее ВТ. // ФТТ. 2004. Т. 46. № 4. С. 596.
- Raty J.Y, Galli G. // Electroanal. Chem. 2005. V. 584. P. 9.
- Kruger A., Kataoka F, Ozawa M. et al. // 2005. V. 43. № 8. P. 1722.
- Шевченко В.Я, Мадисон А.Е, Юръев Т.С. // Физика и химия стекла. 2006. Т. 32. № 3. С. 361.
- Озерин А., Зубов Ю.А. // Высокомолек. соед. А. 1984. Т. 26. № 2. С. 394.
- Озерин А Н, Иванов С.А., Чвалун С.Н, Зубов Ю.А. // Заводская лаборатория. 1986. Т. 52. № 1. С. 20.
- Свергун Д.И., Фейгин Л.А. Рентгеновское и нейтронное малоугловое рассеяние. М.: Наука, 1986.
- Svergun D.I. // Appl. Cryst. 1992. V. 25. Pt. 4. P. 495.
- I. // Biophysical J. 1999. V. 76. № 6. P. 2879.
- Ozerin A.N., Svergun D.I., Volkov V.V. et al. // Appl. Cryst. 2005. V. 38. Pt. 6. P. 996.
- Озерин А Н., Музафаров А.М., Озерина Л.А. и др. // Докл. РАН. 2006. Т. 411. № 1. С. 71.
- Kozin MB, Svergun D.I. // Appl. Cryst. 2001. V. 34. P. 33.
- Konarev P.V., Petoukhov M.V., Svergun D.I. // Appl. Cryst. 2001. V. 34. P. 527.
- Martin JE, Hurd AJ . // Appl. Cryst. 1987. V. 20. P. 61.
- Тинъе А. Рентгенография кристаллов. М.: Физмат- гиз, 1961. 604 с.
- Beaucage G. // Apll. Cryst. 1995. V. 28. P. 717.
- Beaucage G. // Apll. Cryst. 1996. V. 29. P. 134.